Part-8: Polynomial Time Complexity O(n^c)

In our last tutorial we learned about Exponential Time Complexity O(cc). If you have not read it yet please checkout the link below:

Exponential Time Complexity O(cn)

What is Polynomial Time Complexity O(nc) ?

When number of steps required to solve an Algorithm with input size n is O(nc) than it is said to have Polynomial Time Complexity. In simple terms, Polynomial Time O(nc) means number of operations are proportional to power k of the size of input.

Let's look at the diagram:

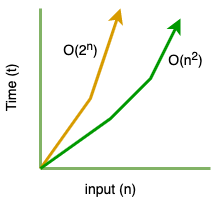
Quadratic time complexity O(n2) is also a special type of polynomial time complexity where c=2. Exponential time complexity O(2n) is worst then polynomial time complexity.

Let's look at how O(n2) grows compare to O(2n): 

When n=10,

O(n2) = 102 = 100
O(2n) = 210 = 1024

As you can see Exponential time complexity O(2n) is worst than Quadratic time complexity O(n2).

Examples of Polynomial Time Complexity O(nc):

Let's look at some examples of Polynomial Time Complexity O(nc): 

// O(n2)
for(let i=0; i<n; i++) {
    for(let j=0; j<n; j++) {
        console.log(i, j);
    }
}

// O(n3)
for(let i=0; i<n; i++) {
    for(let j=0; j<n; j++) {
        for(let k=0; k<n; k++) {
            console.log(i, j, k);
        }
    }
}

// O(n4)
for(let i=0; i<n; i++) {
    for(let j=0; j<n; j++) {
        for(let k=0; k<n; k++) {
            for(let l=0; l<n; l++) {
                console.log(i, j, k, l);
            }
        }
    }
}

I hope you like this tutorial please share and like.

↑