In our last tutorial we learnt about Quadratic time complexity O(n²). If you have not read that article I would suggest you to read it first.

Quadratic time complexity O(n²)

What is Exponential Time Complexity O(cⁿ)?

In exponential time algorithms, the growth rate doubles with each addition to the input (n). Let's look at the chart:

Let's take following example:

function pow(c, n) {
    if (n === 0) return 1;
    return c * pow(c, n-1);
}

console.log(pow(2, 2)); //  4

When we analyze time complexity of above function:

• each simple operation cost 1 unit of time i.e. comparison, multiplication, substraction etc..
• we can ignore other small operations like return statement

Looking at the function we are seeing that there are two conditions here:

• when n=0
• final condition when n=n-1

Here is the function call diagram:

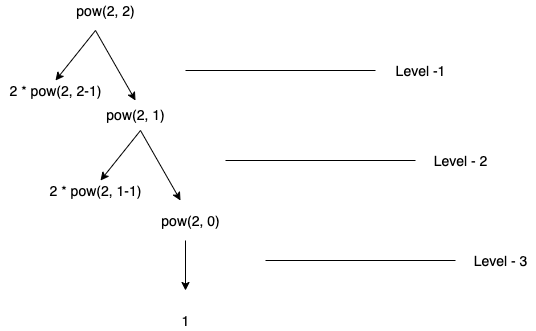
Let say that for above function if we write the equation it would be:

Let say to calculate time complexity of pow(c, n-1) = T(n-1)
Other simple operations that happens in that function is c

T(n) = T(n-1) + c where n > 0 and c = some constant that we need to perform simple operations
T(0) = 1          when n=0 function returns 1

If you want to find:
T(2) = T(n-2) + 2c
T(3) = T(n-3) + 3c
T(k) = T(n-k) + kc

n-k = 0 for base case
then k = n

T(n) = T(n-n) + nc 
     = T(0) + nc
     = 1 + nc because T(0) = 1

T(n) = O(n) considering bigger term from the equation and ignoring other constants

Therefore, total complexity of the statement:  c * pow(c, n-1) = O(cⁿ) which is a bigger term when analyzing out function complexity.