Part-5: Logarithmic Time Complexity O(log n)

In our last tutorial we learnt about Linear Time Complexity O(n). If you have not read that article I would suggest you to read it first.

Linear Time Complexity O(N)

What is logarithmic time complexity O(log n)?

When time taken by an algorithm to run is proportional to the logarithm of the input size n it is said to have logarithmic time complexity. Let's check the following diagram:

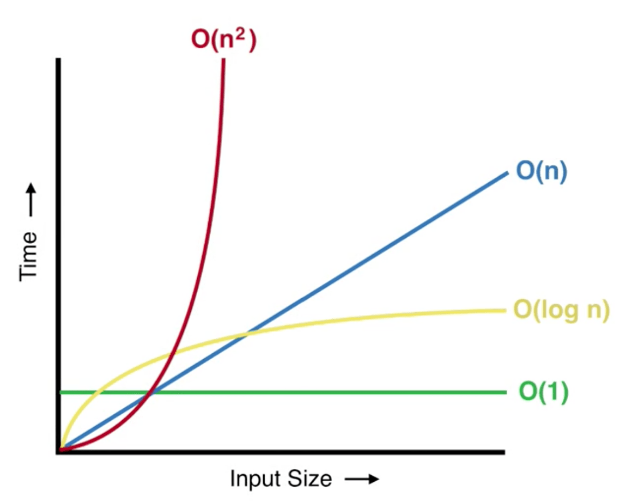
In order to understand this complexity first we need to understand how we can calculate log of some value. So that when we calculate the time complexity of any algorithm we would know if it is logarithmic type complexity or not.

How to calculate log of some numbers?

Let's take following example: 

# Example-1: calculate log216
# basically how many time do we have to multiply 2 to get to number 16
# we need to multiply 2 for 4 times to get to 16
log216 = 2 * 2 * 2 * 2 = 4 times
log216 = log224 
       = 4 log22 
       = 4, because log22 = 1

# Example-2: calculate log327
# we need to multiply 3 for 3 times to get to number 27
log327 = 3 * 3 * 3 = 3 times
log327 = log333
       = 3 log33 
       = 3, because log33 = 1

Now, that we know how to calculate log of some number. We will check out following example: 

for(let i=1; i<n; i=i*2) {
   console.log(i); // O(log n)
}

# when we supply input size n=16 how many times above loop will execute?
# For n=16 i=1,2,4,8, loop will repeate for 4 times when n=16
# you can say that log216 = 2 * 2 * 2 * 2 = 4 times
# therfore, console.log statement will be repeated for log2n

As we know to calculate time complexity of a loop we would have to check how many time statements within a loop are executed. In above case, console.log statement will be repeated for O(log n) times. Therefore, we can say that when we run above code its time complexity will be O(log n).

Find time complexity of following algorithm or program

Let's take following example: 

for(let i=n; i>=1; i=i/2) {
    console.log(i);
}

Let's understand this example in different way, when you look at the loop it starts with i=n. We need to find out how many times it will repeat. So let say that loop will start and end with following order: 

i = n, n/2, n/22, n/23 ............. n/2k

So, i will start from n upto n/2k. We know that loop will stop when i < 1 right therefore we can say that:

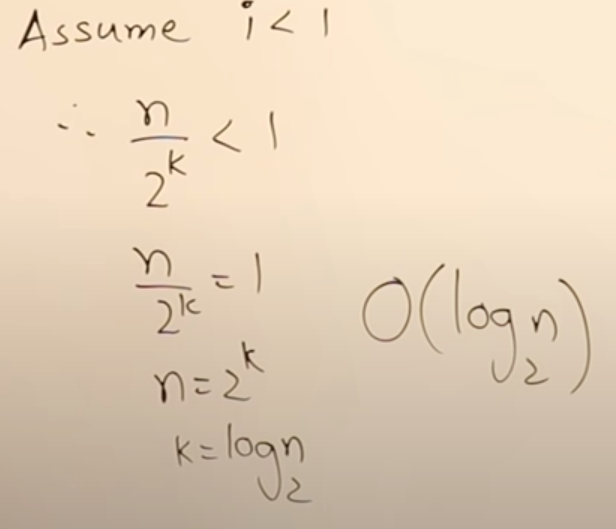
I hope I was able to explain this concept properly.  In our next tutorial we will learn about Quadratic time complexity O(n2).

Quadratic Time Complexity O(N2)

↑