Part-4: Linear Time O(n) Complexity

Before we jump into Linear Time complexity it is very important for you to learn some basics about Big O notation and how to calculate time/space complexity of an algorithm. Read the following tutorial if you have not read it yet.

What Is Big O Notation?

What is Linear Time O(n) complexity?

If you write an Algorithm whoes time execution is dependent on the input size (n) then it is said to have Linear Time O(n) complexity. Let's understant the diagram to visualize the complexity:

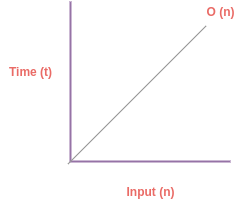
Examples:

  • for loop
  • while loop
  • do while loop
  • foreach loop

Let say that statements within a loops are running with 1 unit of time threfore if a loop runs for n time then it's complexity is = 1 * O(n).

Let's take one practical example to understand more in depth. Let say that we are given a problem to sum of n numbers: 

function sum(n) {
   let sum = 0; // 1 unit of time i.e. O(1)

    for(let i=1; i<=n; i++) { // loop repeats upto n times
        sum += i; // 1 unit of time * n
    }

    return sum; // 1 unit of time
}

// Writing equation
T(n) = 1 + n + 1
     = 2 + n
     = O(n)           // Ingnoring constants and taking upper limit which is n

If you read my last tutorial on big O notation in order to find time complexity of a problem. You need to use following formula:

  • you need to consider each operation = 1 unit of time i.e. O(1)
  • when a statement like loop is repeated n times then
    • all the sub-statements will be repeated n times
  • adding up complexity of all the satements
  • finally, take bigger term from the equation that will be your Big O complexity

You can assume that 1 unit of time = O(1). Therefore above equation can also be written as below: 

T(n) = 1 + n + 1
     = O(1) + O(n) + O(1)
     = O(n) // taking bigger O term from the equation

Other Examples

  • Array insert operation
  • Array remove operation
  • Indexing an array
  • Inserting an array element in middle

Let's look at some examples of O(n) complexity: 

// loop statement which repeats n times
for (var i = 1; i < n; i = i++)  {  // n repetations
   console.log(i); // 1 statement = 1 operation
}

// writing equation
T(n) = 1n (1 opeastion repeated n times)
     = c*O(n) consider c=1 as positive constant
     = O(n)   ignoring constant to get Big O limit

Find complexity of following algorithm: 

function makeLowerCase(arr) {
  if (array.length === 0) {
      return arr;
  } else {
      return arr.map(i => i.toLowerCase());
  }
}

To find complexity of above program we first need to understand how time complexity is calculated:

  • find out number of operation/statement
  • sum all the statements
  • choose bigger term from the equation

Case-1: when array length is zero 

function makeLowerCase(arr) {
  if (array.length === 0) {
      return arr; //  O(1)
  } else {
      return arr.map(i => i.toLowerCase()); // O(n)
  }
}

makeLowerCase([]); // call function with blank array

Alright as we can see above when we are testing our function for blank array it returns instantly because when array size is zero our statement is not dependent of input size of an array.

In this case our function complexity is O(1).

Case-2: when array has some elements 

function makeLowerCase(arr) {
  if (array.length === 0) {
      return arr; //  O(1)
  } else {
      return arr.map(i => i.toLowerCase()); // O(n)
  }
}

makeLowerCase(['ABC', 'DEF']); // size = 2 = n

In above case our array has n elements it goes in else condition of our algorithm and therefore it has to loop through all array elements until it reaches to length of the array.

If we assume that our array has length equals to n then it will have to repeat it for n times. Therefore in this case we get O(n) complexoty. Now, according to Big O we are only concern about the worse case scenario.

Therefore out of O(1) and O(n) we get O(n) as complexity of our problem.

What to remember when calculating time complexity?

  • You have to evalute your algorithm based on worse case when you want to find Big O complexity of a program
  • You will have to find out all cases that your algorithm is designed for an pick the upper limit of big O

In our next tutorial we will learn about Quadratic time complexity O(n2).

Quadratic Time Complexity O(n2)

↑