Arrays are fundamental data structures used to store collections of elements. Searching for an item in an array is a common operation, and choosing the right technique can significantly impact performance.

In this guide, we'll explore different array searching methods, their time complexities, and when to use them—with practical TypeScript examples.

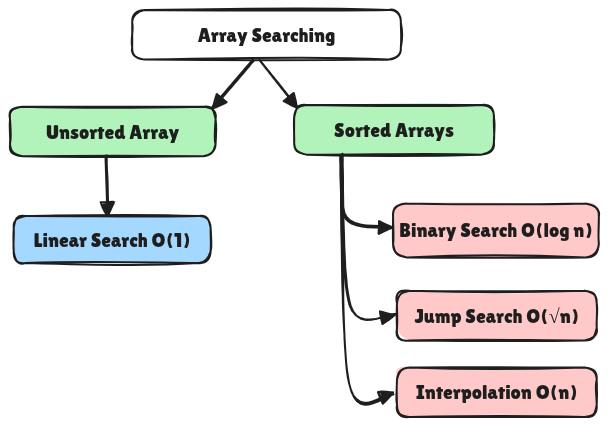
1. Linear Search (Sequential Search)

Linear search checks each element sequentially until the target is found.

• Time Complexity: O(n) – Worst case.
• When to use: Unsorted Arrays with smaller length

Problem: Find a target element inside an array.

Let say that you want to find a target element inside a given array. You need to keep in mind that arrays start at index 0 until length of the array.

When searching in linear direction you start with i=0 and i < arr.length. When we found our target element at given index than we return that index.

function linearSearch(arr: number[], target: number): number {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) return i; // Return index if found
    }
    return -1; // Not found
}

linearSearch([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 5); // Output: 4

2. Binary Search (Divide and Conquer)

Binary search repeatedly divides the array in half, eliminating the need to check every element.

• When to use: Sorted arrays.
• Time Complexity: O(log n) – Efficient for large datasets.

Problem: Find a target element inside an array.

In binary search you define two pointers left = 0 and right = arr.length-1 these pointers they move depending on what part of array contains our target elements.

Target element in sorted array can be either at:

1. Middle of the array
2. Left side from the middle
3. Right side from the middle

Based on this idea we move our pointer each time we halve the array. This search is faster because each time search area is narrowed down by halving the array.

function binarySearch(arr: number[], target: number): number {
    let left = 0;
    let right = arr.length - 1;

    while (left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] === target) return mid;
        if (arr[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

binarySearch([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 5); // Output: 4

4. Interpolation Search

Jump search works by "jumping" ahead in fixed steps and then performing a linear search in the identified block.

• When to use: Sorted arrays where binary search is too complex.
• Time Complexity: O(√n) – Faster than linear but slower than binary.

Problem: Find a target element inside an array.

function jumpSearch(arr: number[], target: number): number {
    let totalSteps = Math.floor(Math.sqrt(arr.length));

    let prev = 0;
    let step = totalSteps;

    while (arr[Math.min(step, arr.length) - 1] < target) {
        prev = step;
        step += totalSteps;
        if (prev >= arr.length) return -1;
    }

    while (arr[prev] < target) {
        prev++;
        if (prev === Math.min(step, arr.length)) return -1;
    }

    return arr[prev] === target ? prev : -1;
}

jumpSearch([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 4); // Output: 3

4. Interpolation Search

Interpolation search estimates the position of the target value, making it faster than binary search for certain datasets.

• When to use: Uniformly distributed sorted arrays.
• Time Complexity: O(log log n) – Best case, O(n) – Worst case.

Problem: Find a target element inside an array.

function interpolationSearch(arr: number[], target: number): number {
    let low = 0;
    let high = arr.length - 1;

    while (low <= high && target >= arr[low] && target <= arr[high]) {
        const pos = low + Math.floor(
            ((high - low) / (arr[high] - arr[low])) * (target - arr[low])
        );

        if (arr[pos] === target) return pos;
        if (arr[pos] < target) low = pos + 1;
        else high = pos - 1;
    }
    return -1;
}

interpolationSearch([1, 2, 5, 6, 9, 12], 12); // Output: 5

5. Using JavaScript Built-in Methods

For quick searches, JavaScript provides built-in methods:

• Array.indexOf() – Linear search.
• Array.find() – Returns first matching element.
• Array.includes() – Checks existence.

Examples:

const fruits = ["apple", "banana", "mango"];

console.log(fruits.indexOf("banana")); // 1
console.log(fruits.includes("mango")); // true
console.log(fruits.find((element) => element === "mango")); // mango

Key Takeaways

• Linear search is simple but inefficient for large datasets.
• Binary search is optimal for sorted arrays.
• Jump search balances simplicity and efficiency.
• Interpolation search excels in uniformly distributed data.

Understanding these techniques helps optimize performance in real-world applications.

For frequently searched data, consider using hash tables (O(1) lookup) or search-optimized trees (e.g., BST, Trie).